Что такое парсер выражений?
Парсер – это программа, которая сопоставляет набор лексем формального языка с его грамматикой. Результатом парсинга является дерево лексем, структура представленного выражения.
Парсер арифметических выражений разбирает исходную строку формулы на составляющие, среди которых могут быть знаки арифметических операций, математические функции и переменные, и вычисляет значение этого выражения.
Для чего нужен парсер?
Люди, которые никогда не слышали что такое парсер, могут спросить: «Зачем вообще нужен парсер?»
Конкретно парсер выражений может применяться в следующих ситуациях:
- При построении регламентированной отчётности в 1С, где определённые строки отчётности складываются по определённым закономерностям.
- Вычисление формул, заданные пользователем в системе.
- Построение отчётов СКД с вычисляемыми полями.
- Динамические алгоритмы, которые можно легко изменить и которые применяются, к примеру, для расчёта сумм документов.
- Разбор выражений в запросах 1С.
Требования к парсеру.
Требования к алгоритму парсера арифметических выражений должны быть следующими:
- Парсер должен разбирать грамматику формального языка за один проход слева направо (в отличие от двухпроходной обработки грамматики в некоторых языках программирования).
- Парсер должен включать в себя как лексический, так и синтаксический анализ исходного текста.
- Парсер должен правильно обрабатывать исключения.
- Парсер должен учитывать приоритет выполняемых операций.
- Парсер должен уметь вычислять стандартные математические функции.
Чтобы лучше понимать на основе какого алгоритма строится данный парсер, рассмотрим теорию построения формальных грамматик.
Формальные грамматики.
Рассмотрим пример простого языка, который определяет подмножество арифметических формул. Формулы могут состоять из знаков арифметических операций, чисел и скобок. Такой язык будет содержать определённые правила построения своей грамматики. В каждом правиле есть левая и правая часть. При этом с левой стороны от знака ? в правиле есть только один нетерминальный символ.
Набор терминальных символов в данном алфавите будет следующим:
{‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’, ‘+’, ‘-‘, ‘*’, ‘/’, ‘(‘, ‘)’}
Нетерминальный алфавит следующий:
{ВЫРАЖЕНИЕ, ЦИФРА, ЧИСЛО, ЗНАК}
Правила грамматики языка:
1. Выражение есть два выражения, соединённые знаком:
ВЫРАЖЕНИЕ ? ВЫРАЖЕНИЕ ЗНАК ВЫРАЖЕНИЕ
2. Выражение есть число:
ВЫРАЖЕНИЕ ? ЧИСЛО
3. Выражение есть выражение в скобках:
ВЫРАЖЕНИЕ ? (ВЫРАЖЕНИЕ)
4. Выражение есть или плюс, или минус, или умножить, или разделить:
ЗНАК ? + | — | * | /
5. Число есть цифра:
ЧИСЛО ? ЦИФРА
6. Число есть число и цифра:
ЧИСЛО ? ЧИСЛО ЦИФРА
7. Цифра есть или 0, или 1, … , или 9:
ЦИФРА ? 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Начальный нетерминал:
ФОРМУЛА
Вывод формулы:
Выведем формулу (25+3) с помощью правил вывода формальной грамматики. Последовательность вывода приведена ниже, каждая текущая замена подчёркнута.
Правило №3: ВЫРАЖЕНИЕ ? (ВЫРАЖЕНИЕ)
Правило №1: (ВЫРАЖЕНИЕ) ? (ВЫРАЖЕНИЕ ЗНАК ВЫРАЖЕНИЕ)
Правило №4: (ВЫРАЖЕНИЕ ЗНАК ВЫРАЖЕНИЕ) ? (ВЫРАЖЕНИЕ + ВЫРАЖЕНИЕ)
Правило №2: (ВЫРАЖЕНИЕ + ВЫРАЖЕНИЕ) ? (ВЫРАЖЕНИЕ + ЧИСЛО)
Правило №5: (ВЫРАЖЕНИЕ + ЧИСЛО) ? (ВЫРАЖЕНИЕ + ЦИФРА)
Правило №7: (ВЫРАЖЕНИЕ + ЦИФРА) ? (ВЫРАЖЕНИЕ + 3)
Правило №2: (ВЫРАЖЕНИЕ + 3) ? (ЧИСЛО + 3)
Правило №6: (ЧИСЛО + 3) ? (ЧИСЛО ЦИФРА + 3)
Правило №5: (ЧИСЛО ЦИФРА + 3) ? (ЦИФРА ЦИФРА + 3)
Правило №7: (ЦИФРА ЦИФРА + 3) ? (2 ЦИФРА + 3)
Правило №7: (2 ЦИФРА + 3) ? (2 5 + 3)
Программная реализация
Моя программная реализация парсера выражений на языке 1С включает проведение разбора следующих операций:
1. Арифметические операции: «+» (сложение), «-» (вычитание), «*» (умножение), «/» (деление).
2. Изменение приоритета операций: «(» (открывающая скобка), «)» (закрывающая скобка).
3. Операции сравнения: «<» (меньше), «>» (больше), «<=» (меньше или равно), «>=» (больше или равно), «=» (равно), «<>» (не равно).
4. Математические функции:
- Цел(x1) – Целая часть числа. Параметры: x1 – исходное число;
- Окр(x1, x2) – Округление. Параметры: x1 – исходное число, x2 – разрядность полученного числа. Если параметр отрицательный, то исходное число округляется до соответствующего разряда целой части;
- Ln(x1) – Натуральный логарифм. Параметры: x1 – исходное число;
- Lg(x1) – Десятичный логарифм. Параметры: x1 – исходное число;
- Sin(x1) – Синус. Параметры: x1 – аргумент функции;
- Cos(x1) – Косинус. Параметры: x1 – аргумент функции;
- Tg(x1) – Тангенс. Параметры: x1 – аргумент функции;
- Asin(x1) – Арксинус. Параметры: x1 – аргумент функции;
- Acos(x1) – Арккосинус. Параметры: x1 – аргумент функции;
- Atg(x1) – Арктангенс. Параметры: x1 – аргумент функции;
- Pow(x1, x2) – Возведение в степень. Параметры: x1 – основание, x2 – показатель степени;
- Sqrt(x1) – Квадратный корень. Параметры: x1 – аргумент функции;
- Abs(x1) – Модуль числа. Параметры: x1 – исходное число;
- Exp(x1) – Число e в степени x1. Параметры: x1 – аргумент функции;
- Pi(x1) – Число пи в степени x1. Параметры: x1 – показатель степени;
- Cmp(x1, x2, x3) – Условный переход. Если x1 >= 0, то cmp = x2, иначе cmp = x3. Параметры: x1 – число, сравниваемое с нулём, x2, x3 – значение условий;
- If(x1, x2, x3) – Условный переход. Если x1 = 0, то if = x2, иначе if = x3. Параметры: x1 – число, сравниваемое с нулём, x2, x3 – значение условий;
- Min(…) – Минимальное значение;
- Max(…) – Максимальное значение;
- And(…) – Логический оператор «И»;
- Or(…) – Логический оператор «ИЛИ».
5. Выделение символьной строки: «’» (апостроф).
6. Переменные таблицы: <Имя столбца>(<Идентификатор строки>). Находит в передаваемой таблице ячейку с определённым значением. Например, функция Об(‘522000’) находит в столбце «Об» в строке с идентификатором «522000» заданное значение. Если такой идентификатор найден не один, то значения ячеек складываются между собой.
Лексический анализатор.
При прохождении текстового выражения используется лексический анализатор, который выделяет из входящего потока символов цельные лексемы: значащие символы, числа, имена функций, операции. Таким образом, встроенный в парсер лексический анализатор используется как фильтр незначащих символов и как построитель цельных лексем, что значительно облегчает разбор выражения.
К примеру, если в тексте выражения попадается число «5.78», то лексический анализатор воспринимает его не как набор символов, а как единую строку. Выражение «5.78 + 7.12» — это соответственно набор 3 лексем: 2 числа – «5.78» и «7.12» и 1 операция – «+». Пробелы в выражении при этом игнорируются.
Далее полученные лексемы передаются синтаксическому анализатору для выделения из формулы её структуры и последующего вычисления значений.
Синтаксический анализатор.
Синтаксический анализатор строит из преобразованного выражения дерево набора лексем с помощью рекурсивного вызова функций, отвечающих за определённые правила. Построенное анализатором дерево свёртывается согласно порядку вызова функций в 1С и на выходе получается одно итоговое значение, которое и является значением всего арифметического выражения.
В коде также представлены некоторые исключения, которые анализируют различные ситуации при разборе выражения. Набор этих исключений в данном случае минимален и не учитывает всяческих «эксклюзивных» ситуаций, но зато покрывает большинство возникающих ошибок.
Обработка 1С.
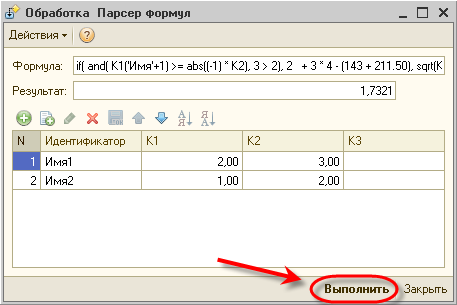
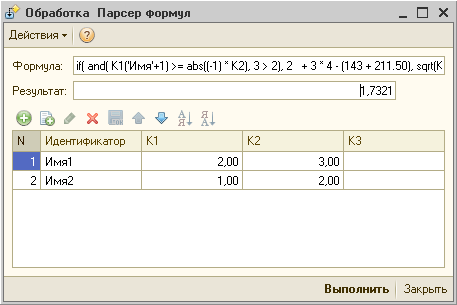
Для примера функционирования парсера выражений создана обработка «Парсер формул». Вводим формулу, заполняем табличную часть и нажимаем кнопку «Выполнить». В поле «Результат» появляется итог вычисления формулы.
В примере используется формула: if( and( К1(‘Имя’+1) >= abs((-1) * К2), 3 > 2), 2 + 3 * 4 — (143 + 211.50), sqrt(К1(‘Имя’+2) + К2(‘Имя2’))).



Автору спасибо.
Здравствуйте,
что озночает kuricapupokparal?
Здравствуйте, Ponchikbar! Вот уж не знаю что вы имеете ввиду :)
Здесь такого слова нет.